Understanding how the Filter function works
Algorithm Fridays Week 2 Solution
What is a filter function and when would you use a filter function in code?
This was the question that more than 25 participants tried to answer in Week 2's edition of Algorithm Fridays - a 39-week initiative aimed at promoting community learning around algorithms and problem-solving.
In this article, I will be explaining how the filter function and using that knowledge, we will see if using the filter function was the most optimal solution for the algorithm problem.
To start off, let's look at the algorithm problem that we worked on for Week 2 of Algorithm Fridays.
Algorithm Problem
The image above shows the algorithm problem for Week 2 of Algorithm Fridays.
Giving this problem a bit more thought and drawing from what we learned last week about doing less work , we can re-interpret this problem to be:
Given an array of numbers, write a function that returns the number of elements in the array nums whose value is not equal to val.
The first step to coming up with this solution will be to filter out those numbers in the array whose values are different from val.
What comes to mind when you think of this? That's right - the filter function!
What is the filter function?
Given a list of elements, the filter function returns a subset of the elements in that list that pass a given condition.
For most languages, the filter function has similar signature. It accepts a callback function that tests each element of the array to see if it passes a given condition.
In JavaScript, the signature of the filter function looks something like this:
const newArray = arr.filter(callback(currentValue[, index[, array]]) {
// return element for newArray, if currentValue passes test
}[, thisArg]);
The filter function is not only common to JavaScript, it also exists in other languages.
While Java also calls it the filter function, C# refers to it to as the Where function while PHP has something similar, called the array_filter function.
How the filter function works
Given that many of the solutions for this algorithm problem leveraged the in-built filter function, it is valuable that we look under the hood to understand how the filter function works.
One really important thing to know about the the filter function is that it creates a new array consisting of elements from the original array that match a given condition.
To test this using JavaScript, run the code snippet below:
const originalArray = [0, 1, 2, 3, 4, 5]
const filteredArray = originalArray.filter((num) => num % 2 === 0)
console.log(originalArray === filteredArray); // This would print false because they are not equal
So, a new array is returned every time the filter function is called because in line with principles of immutability - a core tenet in functional programming, the filter function doesn't mutate the original (input) array passed to it.
What does this mean for the algorithm solution?
It means that using the filter function to solve the algorithm problem creates a new array.
While correct, this is not the most memory-optimal solution. In Big O terms, the solution is O(N) where N is the number of filtered elements; elements in the array that aren't equal to the input value, val.
And since our goal is to do the most with the least amount of resources possible, the question we should be asking is, do we really need to create a new array for this problem?
This brings us to our first solution.
Solution 1 - Loop through and maintain a count of non-equal elements
Since we have re-interpreted this problem as returning the number of elements in the array whose values are not equal to val, there really isn't a need to create a new array.
One solution that avoids creating a new array would entail looping through the elements in the input array and keeping a count of all the elements whose values are not equal to the input value, val.
In JavaScript, the code (without taking care of edge cases) will be something like this:
const getCountOfNonEqualElements = (array = [], val) => {
let count = 0;
array.forEach((element) => {
if (element !== val) count++;
});
return count;
};
In terms of time complexity, this solution is linear - O(N), because we have to iterate through each element in the array.
Awesome! This works, but can we do better?
If we think about it a bit more, the main computation in our solution is iterating through the items in the input array. Is there a way we can iterate through the array faster?
To answer this question, let's look at what our code currently does.
The concept of two pointers
The image below is a graphical illustration of what our code currently does:
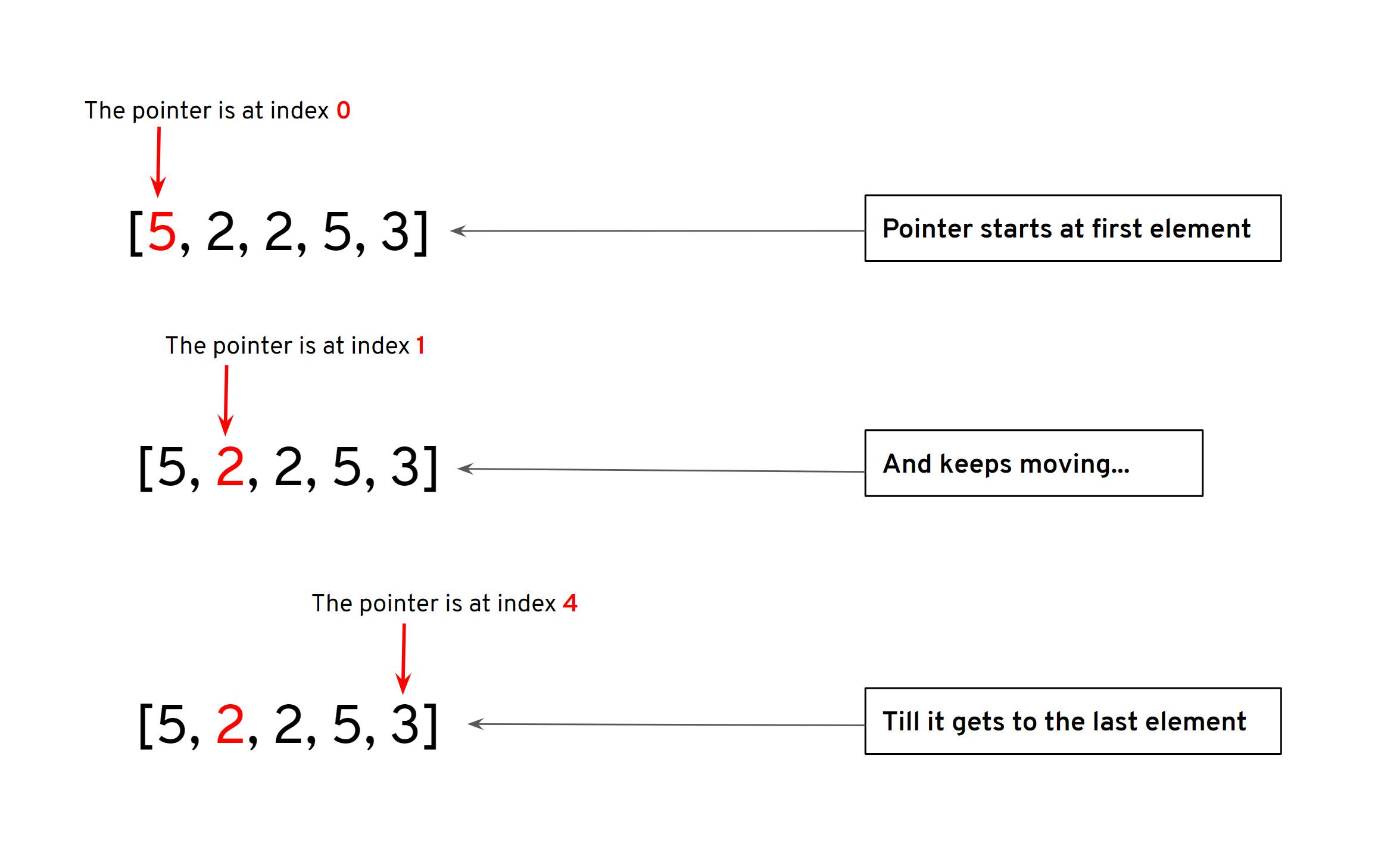
We have one pointer that moves through the array, pointing to one element at a time and checking to see if that element has a value equal to val.
Okay hold on for one second. Is there a reason why we have just one pointer looping through the array? Is it possible to add another pointer to help us move through the array faster?
Can we implement this solution using two pointers? So that while one starts counting from the beginning of the array, the other counts from the end of the array? Because doing that would halve the time needed to loop through the entire array.
That's exactly what the concept of two pointers is about.
Solution 2 - Use two pointers
A second, more optimal solution, will maintain two pointers start and end that will loop through the elements of the input array.
Pointer start will start counting from the beginning of the array whileend will count from the end of the array.
Since pointer start starts from 0 and increments towards the end of the array, we have to be careful to make sure that start doesn't end up doing the same work that end is doing. So how do we keep track of that?
Looking at the illustration below, we see that start keeps moving from 0 to the end of the array while end moves from the end of the array to the start.
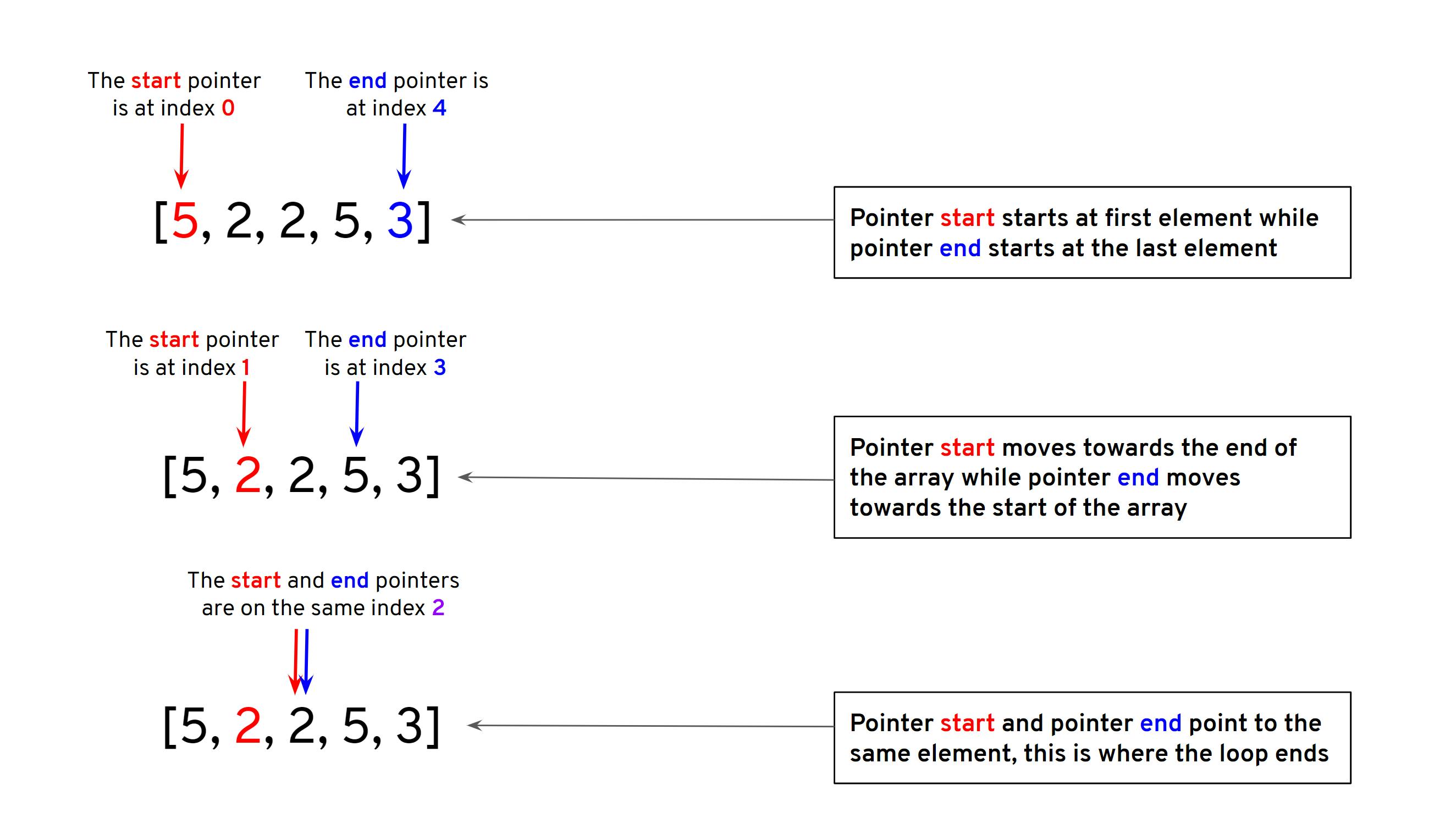
This tells us that as both pointers keep moving, we will get to a point where start and end will either meet (they become equal) and/or they will cross themselves.
This is the point where our loop should end because anything from here on means that either pointer will be duplicating the work the other pointer has already done and we don't want unnecessary work in our code.
The final solution in JavaScript looks something like shown below:
const getCountOfNonEqualElements = (nums=[], val) => {
let countOfNonEqualElements = 0;
// When nums is null or undefined or an empty array
if (!nums || nums.length === 0) { return countOfNonEqualElements };
let start = 0;
let end = nums.length - 1;
while (start <= end) {
if (start !== end) {
// When pointers are not equal,
// check for elements at nums[start] and nums[end]
if (nums[start] !== val) {
countOfNonValElements++;
}
if (nums[end] !== val) {
countOfNonValElements++;
}
}
else {
// When pointers are equal, no need to duplicate the work
// because nums[start] = nums[end]
if (nums[end] !== val) {
countOfNonValElements++;
}
}
start++; // Move start pointer forwards
end--; // Move end pointer backwards
};
return countOfNonValElements ;
};
Winner of the $20 award
After reviewing the 24+ solutions across 4 different programming languages, the $20 award for Week 2 of Algorithm Fridays goes to @freddthink, and here is his solution.
We picked this solution because apart from being correct and robust, it is the most optimal of all the solutions with a time complexity of O(N/2).
A special mention to these solutions: @chygoz2 who implemented a clean O(N) solution with decent error-handling, @ibreathcode who coded an O(N) solution using PHP, @_darkmyke, @techgirlamaka and @tobi_bams who all added decent edge-case checks in their solutions and finally, @TobiAshiru who came up with a O(1) solution in terms of memory usage because he used modified the array in-place .
Thank you once again, to everyone who participated.
Conclusion
Even more important than knowing the in-built functions a programming language provides and when to use them, is knowing how these functions work under the hood to help you write optimal code.
I hope this was worth your read and I hope this spurs you on to read more about your programming language's in-built methods.
Please feel free to share your comments or thought on this post or on the question tweet .
Thanks for reading and see you on Friday for Week 3 of Algorithm Fridays. Have an amazing week ahead!
