How to find the number of unique elements in a sorted array
Algorithm Fridays Week 1 Solution
Introduction
Hello everyone, last Friday was the first of 39 weeks of Algorithm Fridays - an initiative aimed at promoting community learning around algorithms and problem-solving.
Here is the algorithm problem that we worked on last week:
Algorithm Question

We received 20 solutions for this problem, with some really interesting solutions. Before we look the solutions, let's chat a bit about the problem.
Understanding the Problem
To solve any problem, it is important that you fully understand the problem while also ensuring that any assumptions you are making about the problem is correct.
One sure way to do that is to ask the right questions.
Asking the right questions.
To get a good understanding of the problem, it is important to ask the right questions. For this specific problem, here are some questions worth asking:
How important is it for the solution to remove the duplicates from the array? Is it sufficient that the solution only returns the number of unique elements in the array, without needing to remove the duplicates? Because if you think about it, that's really what the problem is about. Since the expected result of the function is the number of unique elements in the array, if we can achieve that with less amount of code, the better. Answering this question strongly determines what the final solution will be.
What is the expected input size? How many numbers will be in the input array? This question is important because the input size determines whether to use a data structure or not for the solution. Most entries that were submitted used a Set data structure; the trade-off with that is that most Sets (regardless of language) have a maximum limit of elements that it can store in memory.
What order is the array sorted in? Ascending or descending? Whatever solution we come up with should work regardless of whether the array is sorted in an ascending or a descending order.
Thinking about edge cases
As software engineers, you always want to avoid the mistake of writing code that only works for the happy-path. Your solution should be as robust as is possible and should be able to handle edge cases.
Some edge cases to think about are:
- What should the expected result be if the input is an empty array?
- What should the expected result be if the input is
nullorundefined?
Solving the Problem
Given that there are two ways we can interpret this problem, there are possibly two solutions:
Solution 1: Removing the duplicates in the array
If we make the focus of the problem to be about removing the duplicates in the array, then one solution would be to use a new data structure to store only the unique elements in this data structure. Most of the solutions submitted used a Set data structure because the set ensures uniqueness.
One interesting memory-optimal implementation of this was by @tobiashiru who did this in-place without having to create a new array. You can view his solution here.
Solution 2: Counting the number of unique elements
If we think of this problem as finding the number of unique elements in the array, then our solution focuses on counting the unique number of elements.
The question now is how do we count the number of unique elements?
Our Solution
For a most optimal solution, we elected to go with interpreting the problem as counting the number of unique elements in the input array.
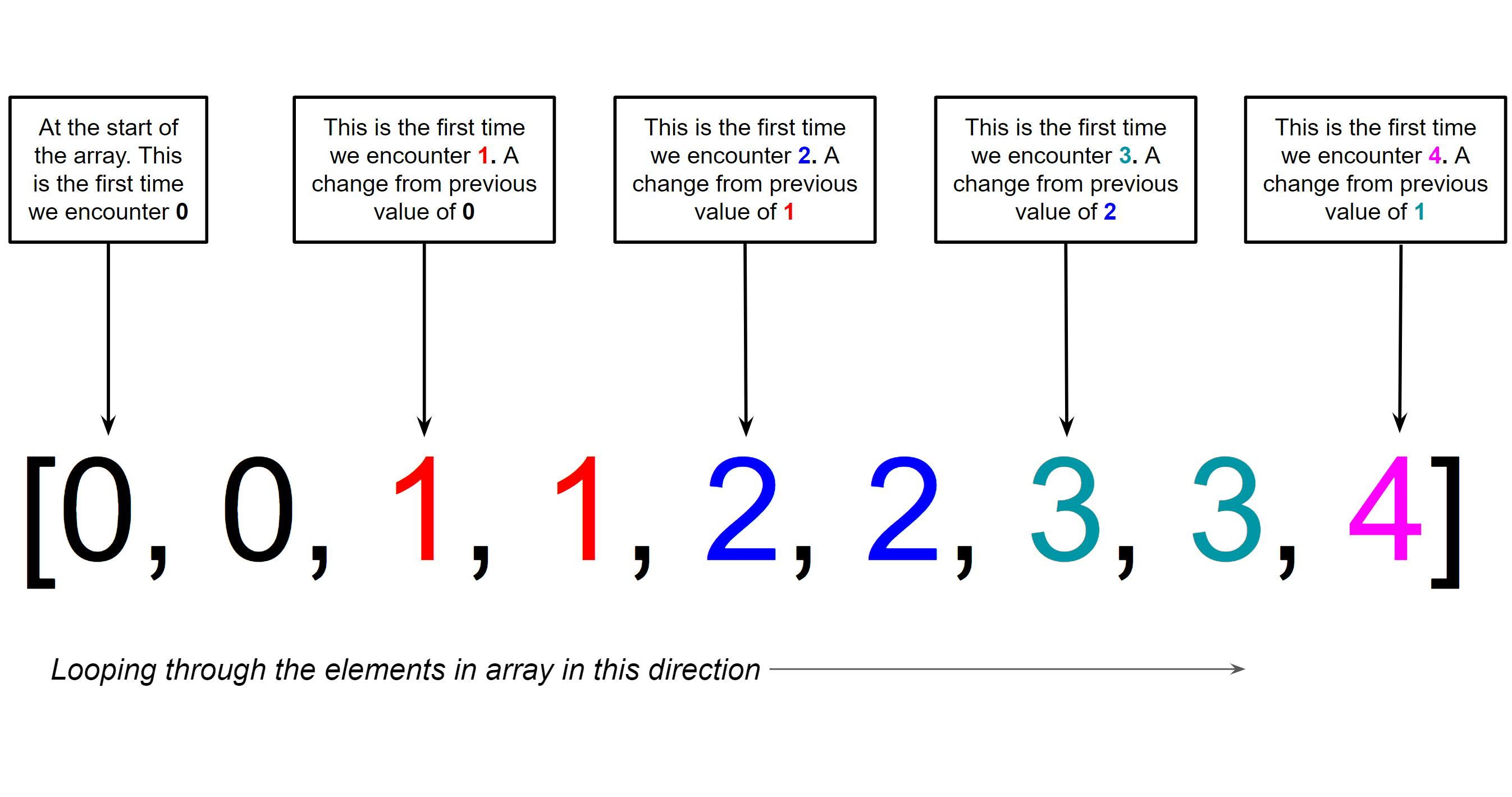
Since the elements are sorted in the array, our solution focuses on counting the number of unique elements by looping through every element in the array and keeping count of the number of times where we encounter a unique number for the first time.
But the next question is: "how do we know when we encounter a unique number for the first time?"
There are two scenarios where we possibly encounter a number for the first time:
- The first element in the array
- Whenever there is a change in the value of the element as we loop through the array.
The image below shows the times we encounter a unique number for the first time.
Below is the coded solution in JavaScript using JavaScript's reduce method:
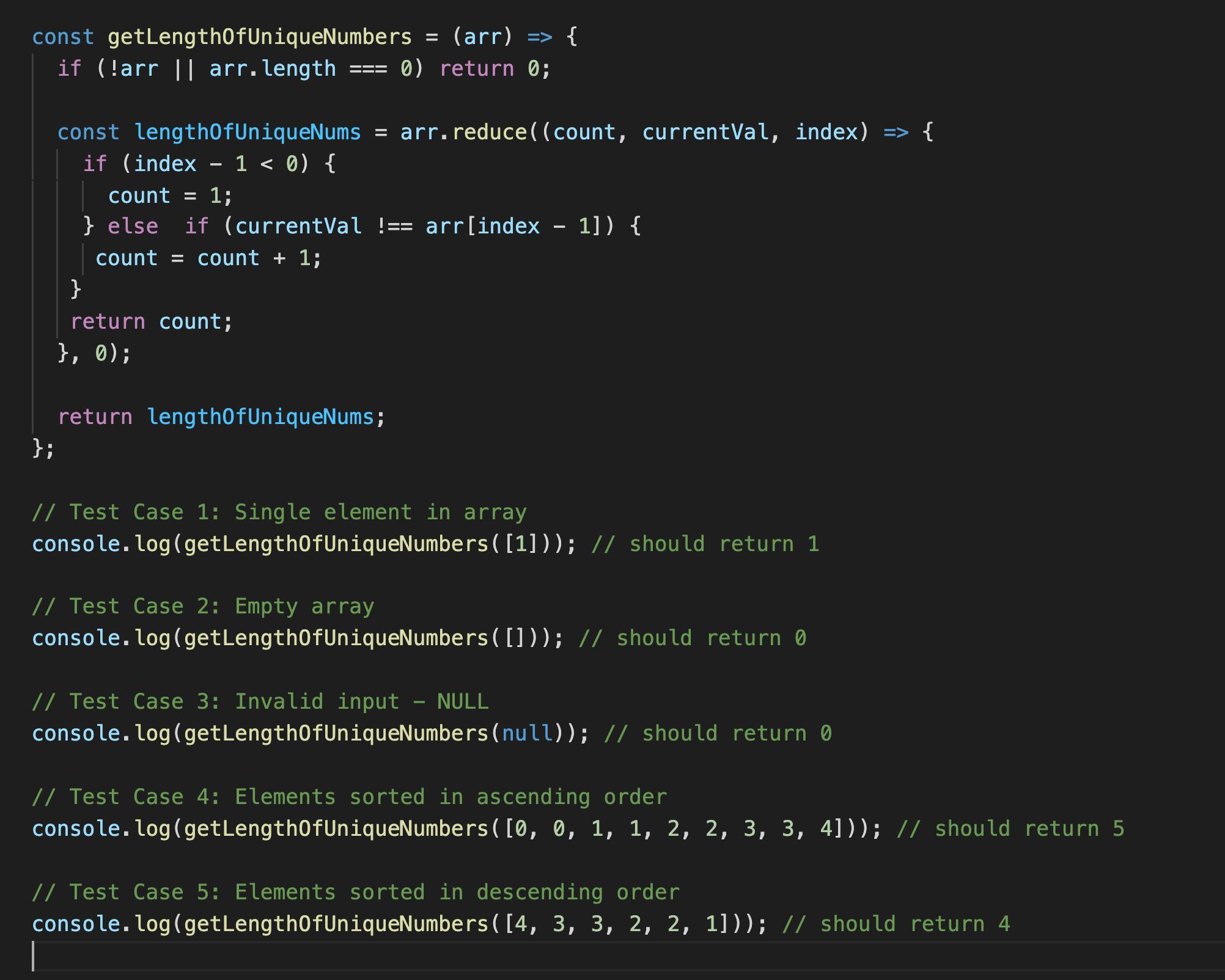
This solution is most memory-optimal because it doesn't use any extra data structure and is linear - O(N), in terms of time efficiency: linear because we have to loop through every element in the array.
Winner of the $20 award
After reviewing the many different solutions and most of which were correct, the $20 award for Week 1 of Algorithm Fridays goes to DeeGenius47, and here is her solution.
We picked this solution because apart from being correct (passed the test cases), it is readable and it is robust - it took care of the edge cases - especially the edge case where the input has a null value, which a lot of the other solutions overlooked.
We also thought to give a special mention to these people: @nxbstxck who added all the different test cases in his solution, @franklin_ezeji whose solution was memory optimal as it didn't use another data structure and lastly, @daviddamilola20 and @bytedeveloper_ who both turned in one-liner solutions.
Finally, thanks to everyone who participated!
Conclusion
As software engineers, our work goes beyond just coding up a solution. Whatever solutions we develop should aim to use the least amount of resources as possible - memory, compute etc.
Equally important as developing a solution is understanding exactly what problem we are solving for and more often that not, this entails asking questions about product requirements in a bid to find the most optimal solution.
I hope this was worth your read and you were able to extract some problem-solving principles that can be applied to other problems even in your day-to-day job. Please feel free to share your comments or thought on this post or on the question tweet.
Thanks for reading and until we meet again this Friday for Week 2's challenge, keep doing more with less resources!

